Category: Math

Categories
Current Events Math

Twitter’s X and other “blackboard bold” letters used in math

By now, you may have heard that Twitter goes by a new name and logo: X. And not just any ordinary X, but an X that looks like this:

This art deco-looking version of the letter “X” isn’t an original design for The Company Formerly Known as Twitter; it’s one of the blackboard bold or double-struck characters used in mathematics, shown below…

…and they’re part of the unicode character set.

Why are these characters called “blackboard bold” or “double struck?”

You may remember sets from your math classes: a concept of a collection of things, each one unique. In math, sets are generally named with a single capital letter, and in math texts, that letter was boldfaced.

Making boldfaced text by hand is tough, especially on a blackboard. In the 1950s and 1960s, a number of math professors started “faking” the bold effect by repeating many of the strokes in a set name’s letter but offsetting them a little. This effect was called “blackboard bold” because it was the blackboard form of bold text. It was also called “double struck” because the effect looked like the text was struck twice with a typewriter.

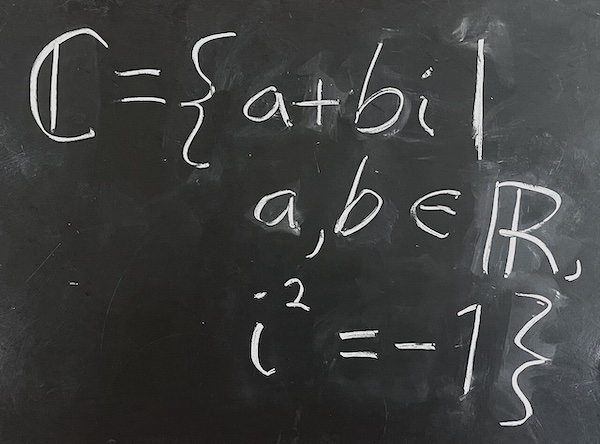
An example of the definition of the set of complex numbers C, with the letters C and R written in blackboard bold.
Creative Commons photo by Jacob Rus. Tap to view the source.

The blackboard bold version of X isn’t used too often, but there are other blackboard bold letters that you might want to familiarize yourself with, especially if your programming starts getting deeper and deeper into math.

Sets whose names are blackboard bold letters

First, there’s N, the set of natural numbers. These are the positive numbers: 1, 2, 3, and so on. They get their name from because they were the first numbers that we “naturally” first came up with.

These were probably our first set of numbers. We used them for keeping count of things that were important to us, such as our children and our livestock (hence the picture above).

Note that 0 is not considered one of the natural numbers, as it is not positive (nor is it negative — it’s in a category all its own).

The next set is W, the set of whole numbers — that’s 0, 1, 2, 3, and so on. It’s basically an expanded version of N, where the expansion is the inclusion of 0. Because it’s a set that contains N, we say that W is a superset of N.

What’s with the old-timey map above? It’s of the spice route, which connected the two peoples who gave us the Hindu-Arabic number system, which gave us the direct predecessor of what we call “zero” today.

Some programming languages have a whole number type that goes by a name like unsigned integer.

Whole numbers leads us to the next set: Z, for Integers. Z is a superset of W, as it includes W and all the negative integers as well. We started using negative numbers around 200 BCE to represent debt (hence the picture of the ledger above).

Why use Z for integers? Because it’s derived from the German word zahlen, which means “numbers.”

Most programming languages have an int or integer type.

The next set is Q, the set of rational numbers. In this case, rational doesn’t mean “based on reason” or “logical” (hence the picture of Mr. Spock), but “ratio,” as in one number divided by another.

Q is the set of all possible combinations of a / b, where a and b are both integers. The “Q” stands for quotient (the result of a division operation).

Believe it or not, Q doesn’t contain every possible number. There are some numbers you just can’t get from a ratio of two integers. These numbers are numbers like π, e, and a number of other numbers that seem to magically define how the universe works.

This set of numbers is P, the set of irrational numbers. They’re not irrational because they’re unreasonable, but because you can’t get them through a ratio.

This is a real place: Ohio State University’s Garden of Constants!

If you join the set of rational numbers Q and the set of irrational number P, you get R, the set of real numbers.

Why are they called “real?” Because they’re not imaginary.

Most programming languages have a real number type — typically, it’s called double.

Imaginary Numbers by Charlie-Unicorn-Fan.
Tap to see the original artwork.

There’s a set of numbers that can’t be quantified — these numbers are called imaginary, and they’re in a set called I.

Examples of imaginary numbers:

  • i, which is the square root of -1. You may sometimes see people using j for the square root of -1; that’s because they’re electrical engineers, who already use i as a variable representing electrical current.
  • Any multiple of i

“Imaginary” is a bit of a misleading name. Technically, all numbers are imaginary! The name comes from mathematicians’ initial discomfort with numbers that when squared, produce a negative value.

And finally, we have C, the set of complex numbers, which are expressed as the following:

a + bi

where:

  • a is the real part of the number, and
  • b is the imaginary part of the number.

Every number is a complex number; it’s just that the numbers we use most of the time have 0 for the b value. For example, the number 3.1415 expressed as a complex number if 3.1415 + 0i.

Complex numbers are typically used in equations where there’s a whole lot of jiggling going on, such as AC current, as well as equations involving light waves or quantum mechanics.

You may be surprised to find out that Python has a built-in complex number type! If you fire up a Python REPL and enter the following…

my_complex_number = 1 + 2j
my_complex_number

…Python will respond with (1+2j). Note that Python uses j to represent the square root of -1, just like electrical engineers do.

Try this:

print(type(my_complex_number))

Python will respond with <class 'complex'>, indicating that my_complex_number is an instance of the built-in complex class.

You can get the real and imaginary parts of my_complex_number by using complex’s real and imag properties:

my_complex_number.real # 1.0
my_complex_number.imag # 2.0

You can find out more about working with complex numbers in Python in this Real Python article.

Categories
Artificial Intelligence Math Programming

You want sum of this? (or: What does the Σ symbol mean?)

If you’ve been perusing LinkedIn or a programming site like Lobste.rs, you may have seen that the professors who teach Stanford’s machine learning course, CS229, have posted their lecture notes online, a whopping 226 pages of them! This is pure gold for anyone who wants to get up to speed on machine learning but doesn’t have the time — or $55K a year — to spend on getting a Bachelor’s computer science degree from “The Cardinal.”

Or at least, it seems like pure gold…until you start reading it. Here’s page 1 of Chapter 1:

This is the sort of material that sends people running away screaming. For many, the first reaction upon being confronted with it would be something like “What is this ℝ thing in the second paragraph? What’s with the formulas on the first page? What the hell is that Σ thing? This is programming…nobody told me there would be math!”

If you’re planning to really get into AI programming and take great pains to avoid mathematics, I have good news and bad news for you.

First, the bad news: A lot of AI involves “college-level” math. There’s linear algebra, continuous functions, statistics, and a dash of calculus. It can’t be helped — machine learning and data science are at the root of the way artificial intelligence is currently being implemented, and both involve number-crunching.

And now, the good news: I’m here to help! I’m decent at both math and explaining things.

Over the next little while, I’m going to post articles in a series called Math WTF that will explain the math that you might encounter while learning AI and doing programming. I’m going to keep it as layperson-friendly as possible, and in the end, you’ll find yourself understanding stuff like the page I posted above.

So welcome to the first article in the Math WTF series, where I’ll explain something you’re likely to run into when reading notes or papers on AI and data science: the Σ symbol.

Σ, or sigma

As explained in the infographic above, the letter Σ — called “sigma” — is the Greek equivalent of our letter S. It means “the sum of a series.”

The series in question is determined by the things above, below, and to the right of the Σ:

  • The thing to the right of the Σ describes each term in the series: 2n + 3, or as we’d say in code, 2 * n + 3.
  • The thing below the Σ specifies the index variable — the variable we’ll use for counting terms in the series (which in this case is n) — and its initial value (which in this case is 1).
  • The thing above the Σ specifies the final value of the index variable, which in this case is 4.

So you can read the equation pictured above as “The sum of all the values of 2n + 3, starting at n = 1 and ending with n = 4.”

If you write out this sum one term at a time, starting with n = 1 and ending with n = 4, you get this…

((2 * 1) + 3) + ((2 * 2) + 3) + ((2 * 3) + 3) + ((2 * 4) + 3)

…and the answer is 32.

You could express this calculation in Python this way…

# Python 3.11

total = 0
for n in range(1, 5):
    total += 2 * n + 3

Keep in mind that range(1, 5) means “a range of integers starting at 1 and going up but not including 5.” In other words, it means “1, 2, 3, 4.”

There’s a more Pythonic way to do it:

# Python 3.11

sum([2 * n + 3 for n in range(1, 5)])

This is fine if you need to find the sum of a small set of terms. In this case, we’re looking at a sum of 4 terms, so generating a list and then using the sum function on it is fine. But if we were dealing with a large set of terms — say tens of thousands, hundreds of thousands, or more — you might want to go with a generator instead:

# Python 3.11

sum((2 * n + 3 for n in range(1, 5)))

The difference is the brackets:

  • [2 * n + 3 for n in range(1, 5)] — note the square brackets on the outside. This creates a list of 4 items. Creating 4 items doesn’t take up much processing time or memory, but creating hundreds of thousands could.
  • (2 * n + 3 for n in range(1, 5)) — note the round brackets on the outside. This creates a generator that can be called repeatedly, creating the next item in the sequence each time that generator is called. This takes up very little memory, even when going through a sequence of millions, billions, or even trillions of terms.

Keep an eye on this blog! I’ll post more articles explaining math stuff regularly.

Worth reading

For more about generators in Python, see Real Python’s article, How to Use Generators and yield in Python.