
Welcome to another installment in my Advent of Code 2020 series, where I present my solutions to this year’s Advent of Code challenges!
In this installment, I share my Python solution to Day 3 of Advent of Code, a.k.a. “The Toboggan Puzzle”.
Spoiler alert!

Please be warned: If you want to try solving the challenge on your own and without any help, stop reading now! The remainder of this post will be all about my solution to both parts of the Day 3 challenge.
The Day 3 challenge, part one

The challenge
Here’s the text from part one of the challenge:
With the toboggan login problems resolved, you set off toward the airport. While travel by toboggan might be easy, it’s certainly not safe: there’s very minimal steering and the area is covered in trees. You’ll need to see which angles will take you near the fewest trees.
Due to the local geology, trees in this area only grow on exact integer coordinates in a grid. You make a map (your puzzle input) of the open squares (
.) and trees (#) you can see. For example:..##....... #...#...#.. .#....#..#. ..#.#...#.# .#...##..#. ..#.##..... .#.#.#....# .#........# #.##...#... #...##....# .#..#...#.#These aren’t the only trees, though; due to something you read about once involving arboreal genetics and biome stability, the same pattern repeats to the right many times:
..##.........##.........##.........##.........##.........##....... ---> #...#...#..#...#...#..#...#...#..#...#...#..#...#...#..#...#...#.. .#....#..#..#....#..#..#....#..#..#....#..#..#....#..#..#....#..#. ..#.#...#.#..#.#...#.#..#.#...#.#..#.#...#.#..#.#...#.#..#.#...#.# .#...##..#..#...##..#..#...##..#..#...##..#..#...##..#..#...##..#. ..#.##.......#.##.......#.##.......#.##.......#.##.......#.##..... ---> .#.#.#....#.#.#.#....#.#.#.#....#.#.#.#....#.#.#.#....#.#.#.#....# .#........#.#........#.#........#.#........#.#........#.#........# #.##...#...#.##...#...#.##...#...#.##...#...#.##...#...#.##...#... #...##....##...##....##...##....##...##....##...##....##...##....# .#..#...#.#.#..#...#.#.#..#...#.#.#..#...#.#.#..#...#.#.#..#...#.# --->You start on the open square (
.) in the top-left corner and need to reach the bottom (below the bottom-most row on your map).The toboggan can only follow a few specific slopes (you opted for a cheaper model that prefers rational numbers); start by counting all the trees you would encounter for the slope right 3, down 1:
From your starting position at the top-left, check the position that is right 3 and down 1. Then, check the position that is right 3 and down 1 from there, and so on until you go past the bottom of the map.
The locations you’d check in the above example are marked here with
Owhere there was an open square andXwhere there was a tree:..##.........##.........##.........##.........##.........##....... ---> #..O#...#..#...#...#..#...#...#..#...#...#..#...#...#..#...#...#.. .#....X..#..#....#..#..#....#..#..#....#..#..#....#..#..#....#..#. ..#.#...#O#..#.#...#.#..#.#...#.#..#.#...#.#..#.#...#.#..#.#...#.# .#...##..#..X...##..#..#...##..#..#...##..#..#...##..#..#...##..#. ..#.##.......#.X#.......#.##.......#.##.......#.##.......#.##..... ---> .#.#.#....#.#.#.#.O..#.#.#.#....#.#.#.#....#.#.#.#....#.#.#.#....# .#........#.#........X.#........#.#........#.#........#.#........# #.##...#...#.##...#...#.X#...#...#.##...#...#.##...#...#.##...#... #...##....##...##....##...#X....##...##....##...##....##...##....# .#..#...#.#.#..#...#.#.#..#...X.#.#..#...#.#.#..#...#.#.#..#...#.# --->In this example, traversing the map using this slope would cause you to encounter
7trees.Starting at the top-left corner of your map and following a slope of right 3 and down 1, how many trees would you encounter?
Importing the data
Every Advent of Code participant gets their own set of data. I copied my data and went through my usual process of bringing it into Python. This involves pasting it into a triple-quoted string and assigning it to the variable raw_input.
raw_input = """...#...###......##.#..#.....##. ..#.#.#....#.##.#......#.#....# ......#.....#......#....#...##. ...#.....##.#..#........##..... ...##...##...#...#....###....#. ...##...##.......#....#...#.#.. ..............##..#..#........# #.#....#.........#...##.#.#.#.# .#..##......#.#......#...#....# #....#..#.#.....#..#...#...#... #.#.#.....##.....#.........#... ......###..#....#..#..#.#....#. ##.####...#.............#.##..# ....#....#..#......#.......#... ...#.......#.#..#.........##.#. ......#.#.....###.###..###..#.. ##..##.......#.#.....#..#....#. ..##.#..#....#.............##.# ....#.#.#..#..#........##....#. .....####..#..#.###..#....##..# #.#.......#...##.##.##..#....#. .#..#..##...####.#......#..#... #...##.......#...####......##.. ...#.####....#.#...###.#.#...#. ....#...........#.##.##.#...... .....##...#.######.#..#....#..# .#....#...##....#..######....#. ...#.....#...#####.##...#..#.#. .....#...##........##.##.##.### #.#..#....##....#......#....#.# ......##...#.........#....#.#.. ###..#..##......##.#####.###.## #.....#..##.##....#...........# ##..#.#..##..#.#.....#......#.. .#.##.#..#.#....##..#..#....#.. .#......##..##.#...#..#.......# #....##.##..###..###......##.#. ....###..##.......#.###.#....#. ..##........#........##.....#.. .#..#.....#...####.##...##..... ....#.#.#.....#.##..##.....#..# ..............#.....#...#.....# .#.....#......###...........#.# .....#.#......#.##..#.......... .#......###............#.#.##.. .#.#....##.#..###.....#.##..#.# .......#.#.#..#..#..#...##..#.# .#.###...##.#.#.####.#.#...#... ...#.#....#......##.##.#....... #...#.....##....#........##.... .....###...#.##.#......##.#..#. ..#...##.##.###..#..#......#### .#.##.#..#.##..##..........##.. ..#.#.#..#.#.....#...###.....#. ..#..#.#....#.##.............## .......#..###..#.#...#.....##.# ####.#.#......#..#.##.........# ..........#.....#..##......###. ..#..............#...#..##..... ......#.#.#..#.##.....####..##. .##.#..#.#....#.......#..#..... ..#..#..#.##.#....###.#.#.#.#.# .....#....#......###..#........ #.#.#..#...###.....#......#.##. ...#.#....#.#......#........#.. ..#...###.#...#..#....##...#..# .###.##..#..#...###.#..#.####.. #....#..##..##..#......#...##.. #.#..#...#..#...###..#.#.##.... ##....#....##.####...#.#.###... ##.#...#.......#.##.##....#...# ..#.#..........#..#.#.#....#..# ..#........#...#....#....#....# ..#..#....#.......#........#... ......#....#....##.#....#.#.##. .##...###.##.##....##.#...###.. .....##..#.#.....###..#.....### ....##.#.##...##..##........#.. #...#..##.#.#....#......#...#.. .###.##.#........#.####....#... #.##.....#..#...#..##.##..#.#.. .....#.#..#....#..#...##.##.#.. .#......#####...##...#.#.###.#. #......##....#.....#......##.#. #.#.##.###.#......#####..#..... ........###.#...#..#.#........# ....#....###..#.##.#...#....#.. ..........#..#.#....#...#.#...# #.##......###.#.#.#....####...# ...#.#....#........##.#.....##. .....##..#.#.#..###...##...#... #...#...#....#....##........#.. .....#.........##.#......#..#.. #.....##..#.###.....#....##.##. ...#..#..#.#........##...##.#.# ..#..##.###.....#.#.....###.##. ..###.........#...##.....###... ...###...##.#...##....##....... .#.#..#...###..#.#....#....#... ##..#.......#....#.#...#..#..#. ..#......#....####..##..#.###.# ..#.......##........#.#.#..#... .#.......#.##.#.##.#.......#..# ###...#...#...#...#..#...#...## ..#..........#..###........##.. .##..#....##......##........#.# ......#.##......#......##...#.# .#.#....#.#.#........#......#.. .#.#..#....####..##...##....#.. .#...##..#..#..#####....##.#... .##.#.#...#...#.#...#.##.#...#. ###.#...##..#.###.#.....#.##.#. #.....#.###.#.#...#..#....#.#.. ..##..#....#......#.........### .#...#...##......#...#.####.... ..#.##...##..............#.#..# ..#......#..##...........#..#.# ..#####...#..#.......##...###.. ..##..#....#.#...###.#...#..... ..#....#..#.#.......#..#.#.#... .##..#.#.....##....#.......#... ...#.#..###...##....#....##..#. .....##..#...##.####....##...#. .......#.........#...#.##..#### ........###..#..#.##.###..#.... .#.#..#.##.##.........#...#.... .###......#.....#....##....#### .##..##...........#.....#.....# #.#.#.#.#.#.##..#.#.#..#.##.... .##.##...##..#....##..###..#### #..##.#......#...###.........#. #..#...#..##..#..##.....##...#. #...##..#...##.#.###.#...#..... .###.....#.......#...#.##.###.# ..........#.#......#...###...## ..##....#.#..#....#.###...#..## #.#..#....##.##..##.........##. #.....#.##.###.#..#....##...#.. ...#........##...#..###..###### #..#.#.#.#...#....#....###.#..# ...##.##.##.....##..#........#. ..#.#....#..#.......#...##.##.# ###.##.......##..#.####...#.#.. ....#.#.....##.....#.#.##...#.. .#..##..#.....#.#..#...#..#..#. .###....##...#......#.....#.... ##.##.###......#...#...###.#... #...#.##...#.#....##.....####.. #.#.#.#...###...##............. ..#....#.....##.#...#......#... ....#...#......#...#..#...#.#.. .###..#.....#..#...#....#...#.. ..#...#.#..###.......#..#.#...# #...###.##.....#....#..#.#..##. ...#.##.#.##......#.#.#.##..... ........####...##...##..#....#. .#.#....#....#.#...##.###...##. #.#...###.#.#.#....#....#.#.... .####.#..#.#....#..#.#..#..#... #####...#...#...#....#.#.#..##. ..###.##.###...#..........#.##. ##.....#...#....###..###.#.#.#. #..##.#..#..#..#...#.#...###..# ##....#.#...##......#.#...#...# .##..........#.#....#...#.##..# ....#....####.#.####......#.### ..##.#.....####.#.####.......#. #.##.##.#.....#.##......##...#. ......###..#.....#.....##...... ..#..#....#.#...#.....#......## ##..#..#..###.#.#..#..##.....#. #....#.#.....#####...#.#....... .....#..#....#.#.#..#...#...#.. ............#.##......##.##.#.# ....#...#.#........###....#.... ..#..#...###.#....##..#..###.## #.##....#...#.....##..#.##.#... ...##..###...#.#.....##.#...... .#..#.##.#####..#.......#..###. ...#.##...###.....####.#.#..... .#......##.#.#.#.#.##.#.....#.. ..#.##.#..##.......#.#.....##.. ..................#....#...#... .##.#..#.#.#..#.......#.#..##.# ....#........#......#..####..#. #...#...##..##.#..#.......##... #..#..#..#..#........####..#.#. ..#.#......#..#.##.##.#.#...#.# ...#..#......#.#.###.#.##..##.. ..#...##.....#..#...##..#.#.... #.........#....#..#....##.##..# ..#..#.#....#..#...#.##.....#.. ...#..#...#.#.....#..##..#.#... ....#........#.#....##..##..#.. #.....#.#..#.......#.##.....#.. .#.###.###...##...##..###...#.. .##.##.......#.#......#.....#.# ...#....##....#..#..........#.# ..#.##.........#.#.....#.....#. ...#.##..##.......##..##...#... #.##......##.##..#.....##...##. #.#.#..##...#.#............#.#. ....#.....#......##...#.#.....# ...#.#......#.#...###.......#.. ......##..###....#.#...#.#####. ..#..#.#.#...##.#...###..##..#. ##.##.#.#.##.#..#....#...#...#. #..#....######.##.#...#...#.#.. .#..#.##....#..#.#.......#....# ....#....#......##....##.#.#... .###......#..#..#.......####..# .#.#.....#..###...........##... .##..##.##.....####..#..#..##.. ..#..##.#......#...###.##..#.#. ....##..#.....###..#.##....##.# #..#......#....#.........#..... .#...#.....#.#..#..##....#..... .##..#...#..##.#..#...........# ..#..##........##.......#..#... #.....#....#....#.#.#...##.#... ...#...#.#.#..#.##.#.#...#..... ..#..#.#....#....###....#.#.#.. ...###..#...#..#....#.....#.... ...#...#.#..#.....#...###...... ##......#..........#.#.#..#.#.# ....#.....#.....#..#..#.#.#.#.. ...####...#.##...#.#..#....#.#. #.##........##.............#.## #.#.#.#.#.....................# .#.###....#..##.##.##....#..... #.#...#.####.###...#..#..#.#... .##...#..###.......##..#.#..... #.#.#.#...#...#.##.....#....... .##.#.#.#......####..#.#....... ###..........#......#...##...#. .........##...#.##...#.#....... ...#.#.....#...#..#...#..##..#. .#..###...#.#.........###....#. ##..#...#........#.........##.. .....#...#.#...#.#.#........... ..#....##...#.#..#..#.##....##. .##....#.#.....##.#..#..#...##. ..##......#.#...#.#.......##.#. ##...#..#...##.#........#.##... #......#.##..#.#..#.###.......# #.#...#.....#.#......#.#.#..... #.....#..#.......#....##.#.#..# ###.#....#..##.#.##....#....#.. #.##.##....#.#..#.#...#....#... ####...#####...#.....#....##.#. ....#.#...#.#.##.#.#.##.#.#.### #.....##.#.....#.#......#.#..#. .#....##.#..#........#...##.#.. ......#...#....##....##....##.. ..###.....#....##.#...#..#..... #....##...##.##..##.#...#...#.. #..#...#...#.#....##..#.#....#. ......................#.....#.. .#..#...#.........#....##...### .##.#.#...##...#...#...#..#.... .#.###....#.#............##..#. ###..##.#.#.#.#....##...#...... .##................####...##.## .#.#.........##....#.#.##.##.#. ....#...#...#...##...#.##.#..#. .#.#........#..##.....#..#....# ##.#..#.#....#.....#...#...#... .#...##....#.....##....#..#.#.# ####.....#..#....#......###.##. ##..##.#....###.....#...#...... .##.#...#.....#.#..#.#..#.#...# .....#.#..#..#..###.#...###.#.. .#.#.##.#..#.#..#...#..#....... ..#.....#....#.##.##.##.......# .#..##....###...#.............. #....#...#.#.......#....##.#... ....#.#..##.#....#..#.#....#.#. #.........##...#.#............. #.#.......##.....#...##..##.#.# .......#....#..##...#..#######. .#.#...##........#..#.....#.#.. .#.......#..#......#.##.##...## .........#............#....#..# .#......#...##...##...#....###. .........#...#.#.###.......#... ###.#..#.#.#.#......##...#.#... .#.........##.#....###....#.#.. #.#....#..#.##.#..#....##...#.. ###.#...#..#..##........#.###.. .....#....#..#........#..#.##.# ..#.....##......#....#..#.#.#.. .#.........#.....#.....#....... ......#....#.###..#.#....#....# ..#.#..#.#.###.........#..#..#. ..#..#.#.#.........#....##.#.#. #.......#........##...##....#.. ##..#..#...###...#..##..#..#.#. ##..#..#....#.#..##..#..#.#..#. ..##.....##.#..#.#........###.. ..#.#..#..##........#...#....## .##..#....##..#..#..#..#.#....# #....#.....##........#.....#.## ......#....#.#..#......#.##.... .......#..#..#......##......... ......#...#..##.....#......#..# #..#..#....##....#........##..# ##....#...#.#.....#####........ ...#.#..#.#.##.#.##..##...#.... ..#..#..#..#..#....#..#..##...# .#.....#....##.##....##.....#.. #...#.....#.....#.#...#.#....#. .###...#..##....#..#...#.###... ....#..##..#.......#.##.##..### #.......##.....#.......#.#...## #.....#.#.#....#.#......#.#.#.. ..##.....#..###......##........ .....#...#..##....#......#..... #..#..#....#.#...#..###.......# .....#.....#....#..#...#.#..##. #####........#...#..#..##..#.#. .#..#...#.##....#.#..#......### #.###.#..#.....##..##....#...#. .#...#.#####....##..........##."""
I then split() the string into a list, using the newline character as the delimiter. I named the resulting list map_basis, since it’s the basis for a complete map of the hill:
map_basis = raw_input.split("\n")
I did a quick len(map_basis) check to see how long a list I was dealing with. It had 323 items.
Strategy
Looking at the question, it became clear to me that the most important problem was to come up with the answer to this question:
Given a set of coordinates, is there a tree at that location?
First, let’s consider the coordinate system of the problem. It’s not unlike screen coordinates, with the origin — (0, 0) — located at the upper left corner of the screen. x increases as you go right, and y increases as you go down:
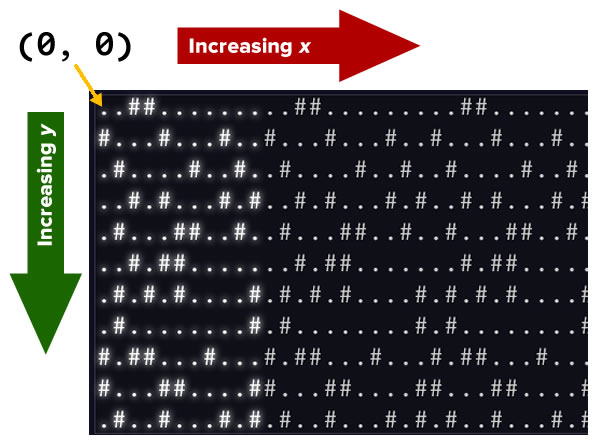
All the strings in map_basis are 31 characters wide, and the actual map repeats itself in the x-direction starting at character index 31. This means that for any given line:
- The character at index 31 is the same as the character at index 0.
- The character at index 32 is the same as the character at index 1.
- The character at index 33 is the same as the character at index 2.
- The character at index 34 is the same as the character at index 3.
- And so on…
This means that for any x-coordinate on the actual hill (let’s call it x_hill_coordinate), its corresponding x-coordinate on the map (let’s call it x_map_coordinate) can be defined by:
x_map_coordinate = x_hill_coordinate mod 31
The map doesn’t repeat itself in the y-direction. Any y-coordinate on the actual hill has the same corresponding y-coordinate on the map.
With that in mind, I defined this function:
def is_tree_at_coordinates(hill_x, hill_y):
map_x = hill_x % 31
return map_basis[hill_y][map_x] == "#"
This function should return True if and only if there is a tree at the coordinates (hill_x, hill_y).
Going down the hill
Now that I had a function that could tell me where the trees were, it was time to go down the hill! I wrote this function, which takes arguments for rightward and downward movement for each “step”. It then “travels” down the hill, counting trees along the way:
def tree_count_for_slope(right_increment, down_increment):
right_coordinate = 0
down_coordinate = 0
tree_count = 0
while down_coordinate < len(map_basis):
if is_tree_at_coordinates(right_coordinate, down_coordinate):
tree_count += 1
right_coordinate += right_increment
down_coordinate += down_increment
return tree_count
For my input data, the tree count was 230.
The Day 3 challenge, part two

The challenge
Here’s the text of part two:
Time to check the rest of the slopes – you need to minimize the probability of a sudden arboreal stop, after all.
Determine the number of trees you would encounter if, for each of the following slopes, you start at the top-left corner and traverse the map all the way to the bottom:
- Right 1, down 1.
- Right 3, down 1. (This is the slope you already checked.)
- Right 5, down 1.
- Right 7, down 1.
- Right 1, down 2.
In the above example, these slopes would find
2,7,3,4, and2tree(s) respectively; multiplied together, these produce the answer336.What do you get if you multiply together the number of trees encountered on each of the listed slopes?
In completing part one, I had also completed the crucial piece of part two! Let this be a lesson to Advent of Code participants: Creating a good data structure or interface for the input data will make coming up with the answers that much easier.
The solution was simply to plug in the values above into my tree_count_for_slope() function and multiply the results together:
print(
tree_count_for_slope(1, 1) *
tree_count_for_slope(3, 1) *
tree_count_for_slope(5, 1) *
tree_count_for_slope(7, 1) *
tree_count_for_slope(1, 2)
)
This gave me the solution for my data: 9533698720.
And with that, I had completed Day 3!
If you have any questions, feel free to post them in the comments.
One reply on “My solution to Advent of Code 2020’s Day 3 challenge, in Python”
[…] My solution to Advent of Code 2020’s Day 3 challenge, in Python […]