This is the second in a series of articles where I’ll get you started on the basics of data science with Python. In this article, we’ll take our first step in building recommendation systems: determining how similar people are by measuring the Manhattan distance between them.
You’ll want the following before you proceed any further:
- The previous article. It’s a good introduction to the series.
- The book: A Programmer’s Guide to Data Mining: The Ancient Art of the Numerati — it’s free to download, and it’s the book we’ll use for the next little while.
- Python 3: Yes, you may have Python 2 on your system right now, but it’s 2018. Get Python 3 — preferably Python 3.6 or later.
 Chapter 2 of A Programmer’s Guide to Data Mining: The Ancient Art of the Numerati is about building recommendation systems. Many recommendation systems are based on a simple idea:
Chapter 2 of A Programmer’s Guide to Data Mining: The Ancient Art of the Numerati is about building recommendation systems. Many recommendation systems are based on a simple idea:
People similar to you often like similar things.
Their trick is to find people who like things that you like, and show you things that you might not have seen yet. For example, here’s a screenshot from my Amazon account, which shows Kindle magazines they’ll think I’ll like, based on my browsing, purchasing, rating history, and who-knows-what-else:

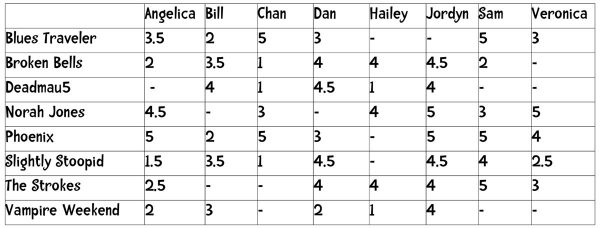
The chapter’s exercises in building a simple recommendation engine make use of the information in the table shown below, which shows 8 people’s ratings of 8 bands that you’d likely hear on an alt-rock station circa 2012:
Click the table to see it at full size.
Each person has rated a number of the 8 bands on a scale of 1 (“hate them”) to 5 (“love them”). No one in the group has rated all 8 bands.
Your first question — and the question we’ll try to answer in this article — should be “How do I tell how similar any two people in this table are?”. I’ll start with some theory, but you’ll see actual code by the end of the article.
Similarity and distance

Before explaining how to figure out how similar any two people in the 8-by-8 table of people and bands are, Zacharski (the author of A Programmer’s Guide to Data Mining: The Ancient Art of the Numerati) starts with a simpler data set: three people, who’ve rated two books on a scale of 0 (worst) to 5 (best): the cyber-thrllers Snow Crash and The Girl with the Dragon Tattoo…
| Book | Amy’s rating | Bill’s rating | Jim’s rating |
|---|---|---|---|
| The Girl with the Dragon Tattoo | 5 | 5 | 4 |
| Snow Crash | 5 | 2 | 1 |
If you were to plot each person’s rating for the books as a single point on a two-dimensional graph, with The Girl with the Dragon Tattoo as the x-axis and Snow Crash as the y-axis, you’d get this:
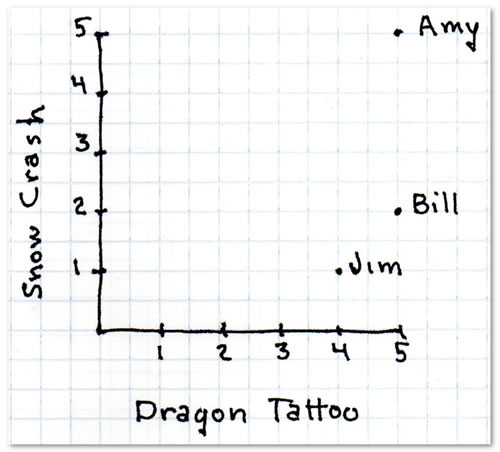
Image from A Programmer’s Guide to Data Mining: The Ancient Art of the Numerati.
The graph makes it easy to see whose tastes are similar. The closer any two people’s points are, the more similar their tastes in cyber-thriller books are. Simply by looking at the graph, you can see that Jim’s taste is more similar to Bill’s than it is to Amy’s, Bill’s is more similar to Amy’s than Jim’s is, and Bill’s is more similar to Jim’s than his is to Amy’s.
While it’s easy for us humans to visually tell whose tastes are similar, it’s much easier to have a program do it mathematically, and there are a number of ways to do it. Let’s look at the simplest way: calculating the Manhattan distance between any two points.
Manhattan distance

There’s a joke about the difference between the directions given to you by Google Maps and Waze: Google Maps will suggest an alternate road to cut down your travel time; Waze will suggest a shortcut through someone’s living room. The Manhattan distance between two points is more like the Google Maps suggestion.
It’s the simplest, computationally least expensive way to compute the distance between two points on a grid. It gets the name “Manhattan” from the way you’d have to travel from one point to another by cab in Manhattan’s grid of streets: only horizontally or vertically, with no diagonals allowed:
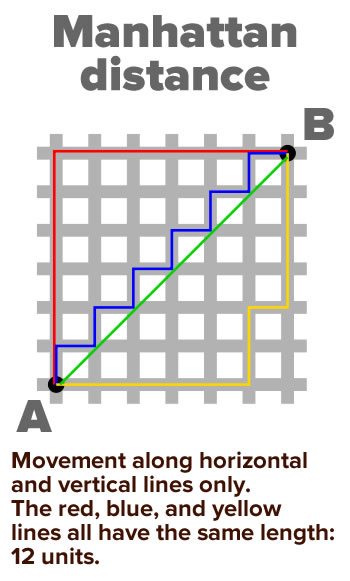
The Manhattan distance between a point located at (x1, y1) and another point at (x2, y2) is simply:
x-distance between the points + y-distance between the points
or, more mathematically:
| x1 – x2 | + | y1 – y2 |
Looking at the Dragon Tattoo/Snow Crash graph…

…we can calculate the Manhattan distance between Bill and Jim:
| 5 – 4 | + | 2 – 1 | = 2
and the Manhattan distance between Jim and Amy:
| 4 – 5 | + | 1 – 5 | = 5
Using Manhattan distance with more than two dimensions
In the previous example, we were dealing with a two-dimensional space, where ratings for The Girl with the Dragon Tattoo form one dimension, and ratings for Snow Crash form another.
Let’s go back to the “people and bands” study and look at two of the people, Jordyn and Sam. Here’s a smaller table that shows only their ratings, and the differences between their ratings for each band:
| Band | Jordyn’s rating for that band |
Sam rating for that band |
Difference between Jordyn’s rating and Sam’s rating |
|---|---|---|---|
| Blues Traveler | – | 5 | n/a |
| Broken Bells | 4.5 | 2 | 2.5 |
| Deadmau5 | 4 | – | n/a |
| Norah Jones | 5 | 3 | 2 |
| Phoenix | 5 | 5 | 0 |
| Slightly Stoopid | 4.5 | 4 | 0.5 |
| The Strokes | 4 | 5 | 1 |
| Vampire Weekend | 4 | – | n/a |
Note that Jordyn and Sam didn’t rate all the bands. To calculate the Manhattan distance between them, we need to work with only those bands that they both rated. Here’s what the table looks like with only those bands:
| Band | Jordyn’s rating for that band |
Sam rating for that band |
Difference between Jordyn’s rating and Sam’s rating |
|---|---|---|---|
| Broken Bells | 4.5 | 2 | 2.5 |
| Norah Jones | 5 | 3 | 2 |
| Phoenix | 5 | 5 | 0 |
| Slightly Stoopid | 4.5 | 4 | 0.5 |
| The Strokes | 4 | 5 | 1 |
Now we can calculate the Manhattan distance between Jordyn’s and Sam’s musical tastes. It’s not all that different from the first Manhattan distance we calculated — it’s simply the sum of all the differences between their ratings for each band, or:
difference between Jordyn’s and Sam’s ratings for Broken Bells +
difference between Jordyn’s and Sam’s ratings for Norah Jones +
difference between Jordyn’s and Sam’s ratings for Phoenix +
difference between Jordyn’s and Sam’s ratings for Slightly Stoopid +
difference between Jordyn’s and Sam’s ratings for The Strokes
which is:
| 4.5 – 2 | + | 5 – 3 | + | 5 – 5 | + | 4.5 – 4 | + | 4 – 5 | = 6.
Given that Jordyn and Sam are rating 5 bands on a scale of 1 to 5 (where 1 is “hate them” and 5 is “love them”), their Manhattan distance can range from…
- 0, which means that they love these 5 bands equally, to
- 20, which means that they have completely opposite opinions of each of the 5 bands.
With a Manhattan distance of 6 (out of maximum of 20) based on 5 bands that are pretty likely to appear on a single Spotify playlist, it would be fair to say that musically speaking, Jordyn and Sam are more alike than dissimilar.
Calculating Manhattan distance, the book’s way
If you remember the previous article in this series or are following along with the book, you know that the “people and bands” data is expressed in code using a Python dictionary, as shown below:
users = {
"Angelica": {
"Blues Traveler": 3.5,
"Broken Bells": 2.0,
"Norah Jones": 4.5,
"Phoenix": 5.0,
"Slightly Stoopid": 1.5,
"The Strokes": 2.5,
"Vampire Weekend": 2.0
},
"Bill": {
"Blues Traveler": 2.0,
"Broken Bells": 3.5,
"Deadmau5": 4.0,
"Phoenix": 2.0,
"Slightly Stoopid": 3.5,
"Vampire Weekend": 3.0
},
"Chan": {
"Blues Traveler": 5.0,
"Broken Bells": 1.0,
"Deadmau5": 1.0,
"Norah Jones": 3.0,
"Phoenix": 5,
"Slightly Stoopid": 1.0
},
"Dan": {
"Blues Traveler": 3.0,
"Broken Bells": 4.0,
"Deadmau5": 4.5,
"Phoenix": 3.0,
"Slightly Stoopid": 4.5,
"The Strokes": 4.0,
"Vampire Weekend": 2.0
},
"Hailey": {
"Broken Bells": 4.0,
"Deadmau5": 1.0,
"Norah Jones": 4.0,
"The Strokes": 4.0,
"Vampire Weekend": 1.0
},
"Jordyn": {
"Broken Bells": 4.5,
"Deadmau5": 4.0,
"Norah Jones": 5.0,
"Phoenix": 5.0,
"Slightly Stoopid": 4.5,
"The Strokes": 4.0,
"Vampire Weekend": 4.0
},
"Sam": {
"Blues Traveler": 5.0,
"Broken Bells": 2.0,
"Norah Jones": 3.0,
"Phoenix": 5.0,
"Slightly Stoopid": 4.0,
"The Strokes": 5.0
},
"Veronica": {
"Blues Traveler": 3.0,
"Norah Jones": 5.0,
"Phoenix": 4.0,
"Slightly Stoopid": 2.5,
"The Strokes": 3.0
},
"GrungeBob": {
"Nirvana": 4.5,
"Pearl Jam": 4.0,
"Soundgarden": 5.0
},
}
Note that I’ve added a ninth person to the list: GrungeBob, who’s stuck in the Pacific Northwest in 1992, and has no bands in common with the other 8 people in the list. He’ll soon prove to be useful.
Here’s the code that the book provides for calculating the Manhattan distance between any two people in the dictionary above:
def manhattan(rating1, rating2):
"""Computes the Manhattan distance. Both rating1 and rating2 are dictionaries of the form
{'The Strokes': 3.0, 'Slightly Stoopid': 2.5 ..."""
distance = 0
for key in rating1:
if key in rating2:
distance += abs(rating1[key] - rating2[key])
return distance
Let’s try out the manhattan() function on Jordyn and Sam:
print(f"Manhattan distance between Jordyn and Sam: {manhattan(users['Jordyn'], users['Sam'])}")
When you run it, you should see the following output:
Manhattan distance between Jordyn and Sam: 6.0
Try calling manhattan() on Chan and Dan:
print(f"Manhattan distance between Chan and Dan: {manhattan(users['Chan'], users['Dan'])}")
Here’s what you should see when you run it:
Manhattan distance between Chan and Dan: 14.0
The closer two people’s musical tastes are, the smaller the Manhattan distance between them is. What happens when you use the manhattan() function to see distance between a person and themself?
print(f"Manhattan distance between Chan and himself: {manhattan(users['Dan'], users['Dan'])}")
Here’s the result:
Manhattan distance between Dan and himself: 0.0
That makes sense — there should be zero distance between two people with identical tastes.
The problem with the book’s manhattan() function
Now what happens when you use manhattan() to get the distance between two people who have no bands in common in their ratings? That’s why I added GrungeBob, who has rated only 3 bands, none of which were rated by anyone else in the group.
Let’s try the manhattan() function on GrungeBob and Jordyn:
print(f"Manhattan distance between GrungeBob and Jordyn: {manhattan(users['GrungeBob'], users['Jordyn'])}")
Here’s the result:
Manhattan distance between GrungeBob and Jordyn: 0.0
The result is 0.0, which should mean that there is no distance between GrungeBob’s and Jordyn’s tastes. But that can’t be — they have no bands in common.
That’s the big problem with manhattan() as implemented in the book. When it produces a result of 0, that result is ambiguous, as it could mean either of the following:
- That the two users compared have identical tastes
- That the two users compared have no bands in common (which suggests that they might have completely disparate tastes)
My solution
I’ll let “Thinking Guy” do the talking for me:

One of Python’s built-in constants is None, the only value in a type called NoneType, and it’s meant to be used to represent the absence of a value. We can use None as the result for manhattan when given two people with no bands in common.
With this in mind, let’s think about the results that manhattan should return based on the users given to it as arguments:
- The simple case: given two users with tastes {“x”: 0, “y”: 0} and {“x”: 1, “y”: 1},
manhattanshould return 2, because their preferences are each 1 unit apart. - The identical user case: given two users identical tastes — {“x”: 1, “y”: 2, “z”: 3} —
manhattanshould return 0, because each of their preferences has no distance between them. A Manhattan distance of 0 means identical tastes. - The case of slightly different tastes, where both users have rated the same bands, but have given them different ratings: Given two users with the tastes {“x”: 1, “y”: 2, “z”: 3} and {“x”: 4, “y”: 5, “z”: 6},
manhattanshould return 9, which is
| 1 – 4 | + | 2 – 5 | + | 3 – 6 |. - The case of slightly non-overlapping tastes, where both users have rated different bands, some of which overlap: Given two users with the tastes {“a”: 1, “y”: 2, “z”: 3} and {“b”: 4, “y”: 5, “z”: 6}),
manhattanshould return 6, which is
| 2 – 5 | + | 3 – 6 |. - The case of completely non-overlapping tastes, where both users have rated different bands, and have no bands in common: Given two users with the tastes {“x”: 1, “y”: 2, “z”: 3} and {“a”: 4, “b”: 5, “c”: 6}),
manhattanshould returnNone.
We can express these specs as tests, which is something that the book doesn’t do, but we will. Here are my tests, as written for Python’s unittest:
def test_manhattan_distance(self):
local_test_users = {
"Local test user 1": {"x": 0, "y": 0},
"Local test user 2": {"x": 1, "y": 1},
}
self.assertEqual(manhattan_distance_between_users(local_test_users,
"Local test user 1",
"Local test user 2"),
2,
"""
The Manhattan distance between (0, 0) and (1, 1) should be 2.
""")
def test_manhattan_for_identical_tastes(self):
self.assertEqual(manhattan(self.test_users, "Angelica", "Angelica"),
0,
"""
The Manhattan distance between two identical tastes
should be zero.
""")
def test_manhattan_for_different_tastes(self):
local_test_users = {
"Local test user 1": {"x": 1, "y": 2, "z": 3},
"Local test user 2": {"x": 4, "y": 5, "z": 6},
}
self.assertEqual(manhattan(local_test_users,
"Local test user 1",
"Local test user 2"),
9,
"""
The Manhattan distance between {"x": 1, "y": 2, "z": 3}
and {"x": 4, "y": 5, "z": 6} should be 9.
""")
def test_manhattan_for_different_slightly_nonoverlapping_tastes(self):
local_test_users = {
"Local test user 1": {"a": 1, "y": 2, "z": 3},
"Local test user 2": {"b": 4, "y": 5, "z": 6},
}
self.assertEqual(manhattan(local_test_users,
"Local test user 1",
"Local test user 2"),
6,
"""
The Manhattan distance between {"a": 1, "y": 2, "z": 3}
and {"b: 4, "y": 5, "z": 6} should be 6.
""")
def test_manhattan_for_completely_nonoverlapping_tastes(self):
local_test_users = {
"Local test user 1": {"x": 1, "y": 2, "z": 3},
"Local test user 2": {"a": 4, "b": 5, "c": 6},
}
self.assertEqual(manhattan(local_test_users,
"Local test user 1",
"Local test user 2"),
None,
"""
The Manhattan distance between {"x": 1, "y": 2, "z": 3}
and {"a": 4, "b": 5, "c": 6} should not be a number,
but the value 'None'.
""")
You may have noticed that my tests define manhattan that takes not 2, but 3 arguments:
- A dictionary of user dictionaries — the set of user’s band ratings
- the name of the first user
- the name of the second user
By requiring the caller to provide manhattan with the complete set of ratings, it removes the method’s dependency on external global variables.
Now that we have tests, let’s write a manhattan function that passes those tests:
def manhattan(all_users, user1_name, user2_name):
distance = 0
common_keys_were_found = False
user1_ratings = all_users[user1_name]
user2_ratings = all_users[user2_name]
for key in user1_ratings:
if key in user2_ratings:
distance += abs(user1_ratings[key] - user2_ratings[key])
common_keys_were_found = True
if common_keys_were_found:
return distance
else:
return None
Try it out on some of the users. Here’s how you get the Manhattan distance between Jordyn and Sam:
print(f"Manhattan distance between Jordyn and Sam: {manhattan(users, 'Jordyn', 'Sam')}")
You should see this result:
Manhattan distance between Jordyn and Sam: 6.0
The result is the same as before, which is what we want. Let’s get the distance between Jordyn and Jordyn:
print(f"Manhattan distance between Jordyn and Jordyn: {manhattan(users, 'Jordyn', 'Jordyn')}")
This should be zero, and that turns out to be the case:
Manhattan distance between Jordyn and Jordyn: 0.0
Finally, let’s check the case that failed with the previous version of the function, the distance between Jordyn and GrungeBob — and remember, GrungeBob has no bands in common with anyone else in the group:
print(f"Manhattan distance between Jordyn and GrungeBob: {manhattan(users['Jordyn'], users['GrungeBob'])}")
Here’s the output for that code:
Manhattan distance between Jordyn and GrungeBob: None
This bit of code will show you the Manhattan distances between Hailey and all the users, including herself:
for user_name in users:
distance = manhattan(users, user_name, 'Hailey')
if distance is None:
print(f"No bands in common between Hailey and {user_name}.")
else:
print(f"Manhattan distance between Hailey and {user_name}: {distance}.")
You should see these results:
Manhattan distance between Hailey and Angelica: 5.0. Manhattan distance between Hailey and Bill: 5.5. Manhattan distance between Hailey and Chan: 4.0. Manhattan distance between Hailey and Dan: 4.5. Manhattan distance between Hailey and Hailey: 0.0. Manhattan distance between Hailey and Jordyn: 7.5. Manhattan distance between Hailey and Sam: 4.0. Manhattan distance between Hailey and Veronica: 2.0. No bands in common between Hailey and GrungeBob.
Next steps
In the next installment, we’ll look at finding the most similar user to a given person, and actually making recommendations. Watch this space!